
Everyone has heard about AI code generation tools and the quality concerns that come with them. I recently started a new company called Ribbon Optimization Software in early February to guarantee safe, efficient code generation for engineering applications. My approach uses a custom code generation framework that acts like a railway. Code is generated based on strict constraints that have been pre-programmed by a human.
Let’s take a look at a current build of what I call the Ribbon Compiler. Presently, it is accessed through the command terminal:
$> rcgen --help
Ribbon Compiler v0.9.1 supported algorithms:
---------------------------------------------
Dense Basic Linear Algebra Subroutines (BLAS)
---------------------------------------------
blas::dense::axpy
blas::dense::dot
blas::dense::norm_inf
blas::dense::norm_1
blas::dense::norm_2
blas::dense::rot
blas::dense::rotg
blas::dense::scale
blas::dense::gemv
blas::dense::triangular_solve
blas::dense::gemm
------------------------------------------------
Sparse Basic Linear Algebra Subroutines (spBLAS)
------------------------------------------------
blas::sparse::axpy
blas::sparse::dot
blas::sparse::gemv
blas::sparse::triangular_solve
--------------------------
Dense Matrix Decomposition
--------------------------
decomposition::dense::cholesky_factor
decomposition::dense::cholesky_solve
---------------------
Function Minimization
---------------------
minimize::dense::unconstrained::bfgs
minimize::dense::unconstrained::newtonChoosing one of these options will ensure that the auto-generated code is at least as safe and efficient as what human expert could write. Let’s single out the decomposition::dense::cholesky_factor algorithm which allows for the efficient solution of dense linear systems of equations (i.e. all entries of the matrix are stored in memory).
Recall that given an N-by-N matrix with the properties
\[A = A^T \quad \text{and} \quad \mathbf{x}^T A \mathbf{x} > 0, \mathbf{x} \in \mathbb{R}^N\]
the Cholesky Decomposition is the unique lower triangular matrix such that
\[A = L L ^T\]
Let’s generate code for a small Cholesky factor routine with the Ribbon Compiler.
$> rcgen decomposition::dense::cholesky_factor --inputs=size:3 --verbosity=info
[rcgen] Fused-Multiply-Add Instructions: on
[rcgen] Vectorized Instruction Max Byte Width: 32
[rcgen] Initialized algorithm variant 'dense_cholesky_factor_stride4_fma_fp64_3_3'.
[rcgen] Created new workspace folder "./rcgen_results_ohTQBK".
[rcgen] No custom file name specified. Using default 'dense_cholesky_factor_stride4_fma_fp64_3_3' for this algorithm with specified parameters.
[rcgen] Beginning code generation for 'decomposition::dense::cholesky_factor'.
[rcgen] Successful code generation for 'decomposition::dense::cholesky_factor'.This generates a file containing assembly code. Unlike more complicated algorithms, these linear algebra operations are often a bottleneck in engineering software. As a result, the default behavior is to streamline these operations as much as possible. My computer has an AMD x86 processor running Linux which produces the following assembly code file.
# Copyright (c) Ribbon Optimization Software LLC 2025-2025
# Code generated by Ribbon Compiler (TM) v0.9.1
# Generated on Mon Jul 7 12:11:21 2025
.intel_syntax noprefix
.bss
.data
.global dense_cholesky_factor_stride4_fma_fp64_3_3
.text
dense_cholesky_factor_stride4_fma_fp64_3_3:
vmovsd xmm0, [rdi]
# Start Processing Column 0:
vsqrtsd xmm0, xmm0, xmm0
vmovddup xmm4, xmm0
vmovupd xmm2, [rdi + 8]
vdivpd xmm2, xmm2, xmm4
# Start Processing Column 1:
# Update Column 1 with Row 0:
vmovddup xmm1, xmm2
vmovupd xmm6, [rdi + 24]
vfnmadd231pd xmm6, xmm1, xmm2
vmovsd xmm5, xmm5, xmm6
vsqrtsd xmm5, xmm5, xmm5
vmovupd [rdi + 24], xmm6
vshufpd xmm6, xmm6, xmm6, 0x3
vdivsd xmm6, xmm6, xmm5
# Start Processing Column 2:
# Update Column 2 with Row 0:
vmovsd xmm3, [rdi + 40]
vmovupd [rdi + 8], xmm2
vshufpd xmm2, xmm2, xmm2, 0x3
vfnmadd231sd xmm3, xmm2, xmm2
# Update Column 2 with Row 1:
vfnmadd231sd xmm3, xmm6, xmm6
vmovsd xmm7, xmm7, xmm3
vsqrtsd xmm7, xmm7, xmm7
vmovsd [rdi], xmm0
vmovsd [rdi + 32], xmm6
vmovsd [rdi + 24], xmm5
vmovsd [rdi + 40], xmm7
ret
# end functionThe final code was generated using human-guided heuristics involving register scheduling, software pipelining and instruction-level parallelism to maximize performance. These codes can become quite long – like Ribbons – which is where the name of the company originates. I sometimes like to call these long functions Ribbon Code. It helps visually emphasize the space/time trade-off being employed.
Calling this code from C is straightforward. Here’s what a C header file might look like.
#ifndef __DENSE_CHOLESKY_FACTOR_STRIDED4_FMA_FP64_3_BY_3_H__
#define __DENSE_CHOLESKY_FACTOR_STRIDED4_FMA_FP64_3_BY_3_H__
#ifdef __cplusplus
extern "C" {
#endif
/* Call x86 Cholesky Factor auto-generated code for 3-by-3 matrix. */
void dense_cholesky_factor_stride4_fma_fp64_3_3( double* A );
#ifdef __cplusplus
}
#endif
#endif /* __DENSE_CHOLESKY_FACTOR_STRIDED4_FMA_FP64_3_BY_3_H__ */General compilers such as GCC and Clang are not algorithm-aware and have difficulty producing efficient linear algebra kernels. As a result, many of these linear algebra kernels are still written in Fortran or hand-coded in assembly. The C++ committee has acknowledged this limitation and added some linear algebra support to the C++26 standard.
Presently, the Ribbon Compiler is targeted at embedded devices with fewer computing resources than a desktop processor. This means that generated programs work best if the linear algebra can fit in L2 cache. To quickly check performance, let’s compare against Intel’s Math Kernel Library (MKL) for small kernels. This is an industry standard for linear algebra performance.
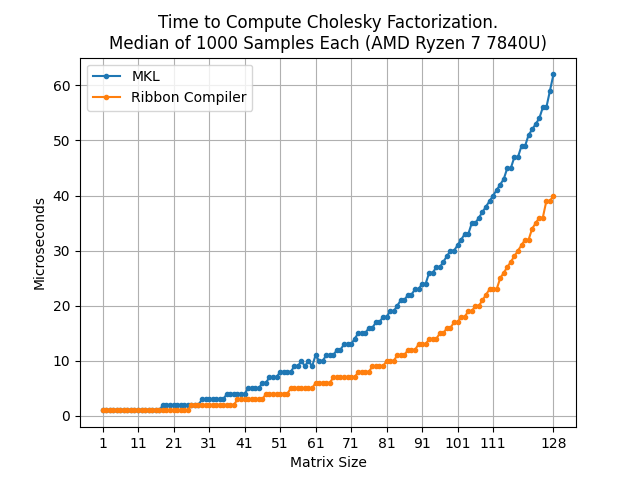
For this AMD CPU, the Ribbon Compiler performs much better. Each core has about 1 Megabyte of L2 Cache which becomes saturated at N=94. At that point, the performance decreases. It is easier to see this in a plot of the speedup.
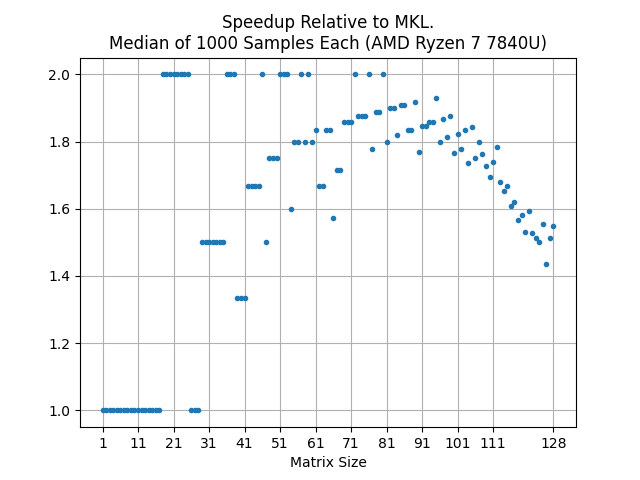
For embedded devices with less memory and limited cores, this is as optimal as one can get with these bottlenecks. Not only that, but the generated code is flexible – it can be easily modified and integrated with existing source code.
One last remark: What if you don’t know your problem size beforehand? This is not an issue. All of this code can be generated at run time. The Ribbon Compiler has an application programming interface (API) that allows for the generation and execution of the same code in RAM. This API was used to produce the timing results above.
In summary, I created Ribbon Optimization Software with the purpose of reducing software development time through automatic code generation. Unlike large language models, my approach is restricted to human-defined guardrails that will always produce safe and efficient code for a given application. This can yield great results when applied to software bottlenecks – even outperforming a titan such as Intel for common applications.
In a future blog post, I will demonstrate how the Ribbon Compiler can achieve even more dramatic performance improvements on sparse matrix algebra (i.e. matricies that contain many zero-valued entries).
If you are interested in learning more about this technology and its uses, please contact support@ribbonopt.com for more information. We would love to understand what kinds of issues you are facing and how these tools can better serve the engineering community.
-Adam